How to use sensors in MSC Adams

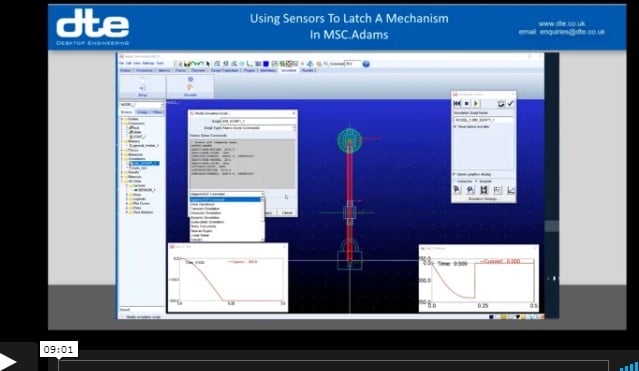
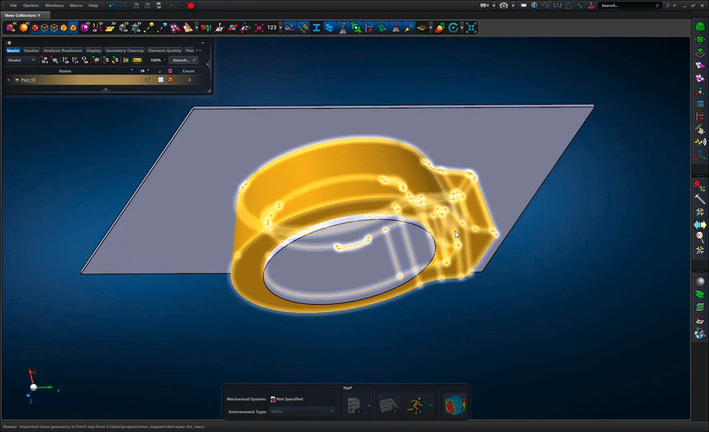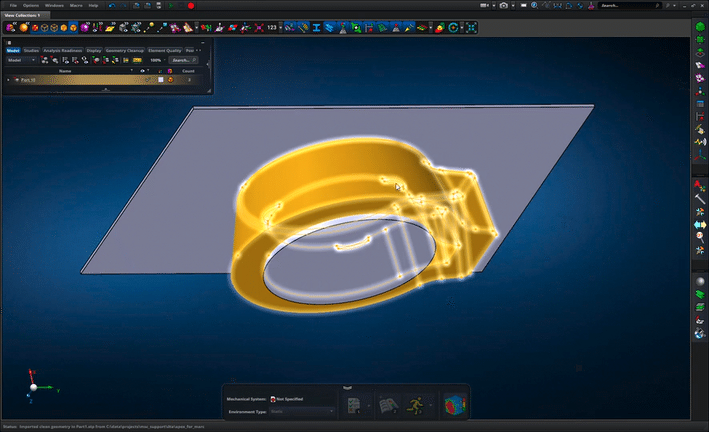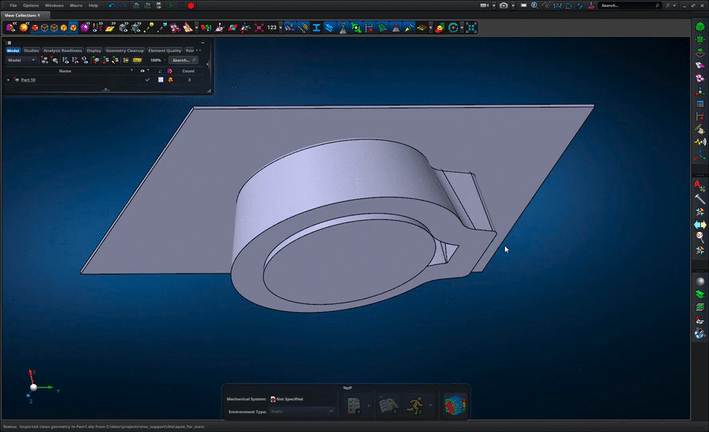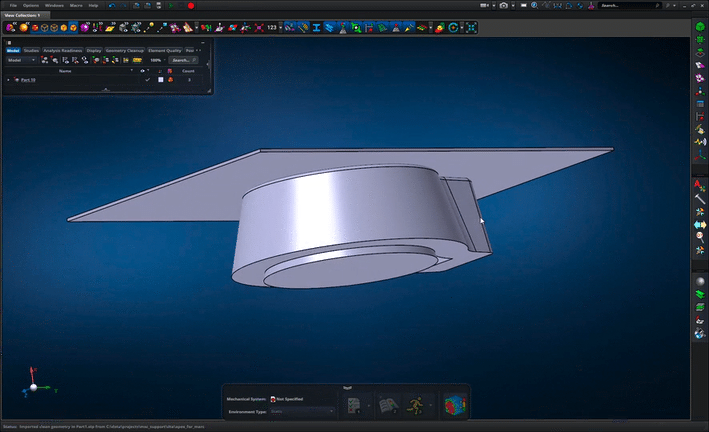
Using Sensors to Latch a Mechanism

Sometimes with a mechanism simulation you need to trigger a change in the mechanism when an event such as a latch engaging to stop a component from moving any further. You can model the geometry and use a contact model to capture the physical engagement of the geometry, but this can add to your simulation run time and require a lot of tuning to get working happily.

Shear Force & Bending Moment Diagrams

Generate output with MSC Apex

Creating Shear Force and Bending Moment diagrams for MSC Software's Nastran can be less than straightforward with the older tools.

MSC Apex has an elegant way of generating this output using existing results that is demonstrated in this short video.

MSC Apex and CAEFatigue for Random Response analysis

MSC Apex is MSC software’s new GUI environment.  It’s been around for a few years and development is progressing steadily. 

While it does an amazing job with model preparation broad support for analysis solutions is still evolving.

Space Sector Benefits

A key area for our customers in the Space sector is around Random Response analysis which is a requirement for predicting the damage caused during the launch event by the launch agencies.

Apex supports the underlying frequency response analysis but full support for pre-and post-processing the Random element for Nastran is not available as of the 2021.2 release. 

Actran Diffuse Sound Field (DSF) demo

Actran, from MSC Software, is an acoustics simulation software, originally designed for predicting noise within, and around vehicles, such as cars and aircraft.  

MSC Apex as a pre-processor for MSC Marc

MSC Apex is first and foremost a pre/post processor for Nastran but that doesn’t stop users of other solver technologies from taking advantage of the model preparation and meshing capability. 

The Nastran bulk data format is the closest thing we have to a universal FEA definition file and so can be read by almost every other FEA application out there. 

Space Technologies - solutions with Heritage

NASA Structural Analysis Code* was just the beginning ..... 

MSC Software has been a key partner to the Space Industry since the 1960s.  Many people associate MSC only with Nastran, which is the keystone of their product set, but through a process of development and acquisition, they have developed a portfolio of tools that are used across a number of domains within engineering simulation in the Space Industry. 

Improve composite FEA process AND get manufacturing output

How to improve your composite FEA process AND get manufacturing output as a side benefit

When working with laminated composites it is important to consider the effects that draping the pre-pregs has on the orientations and thickness that get used in finite element analysis. 

Laminate Modeller is a plug-in tool for MSC Patran that does this fundamental job, but offers so much more. 

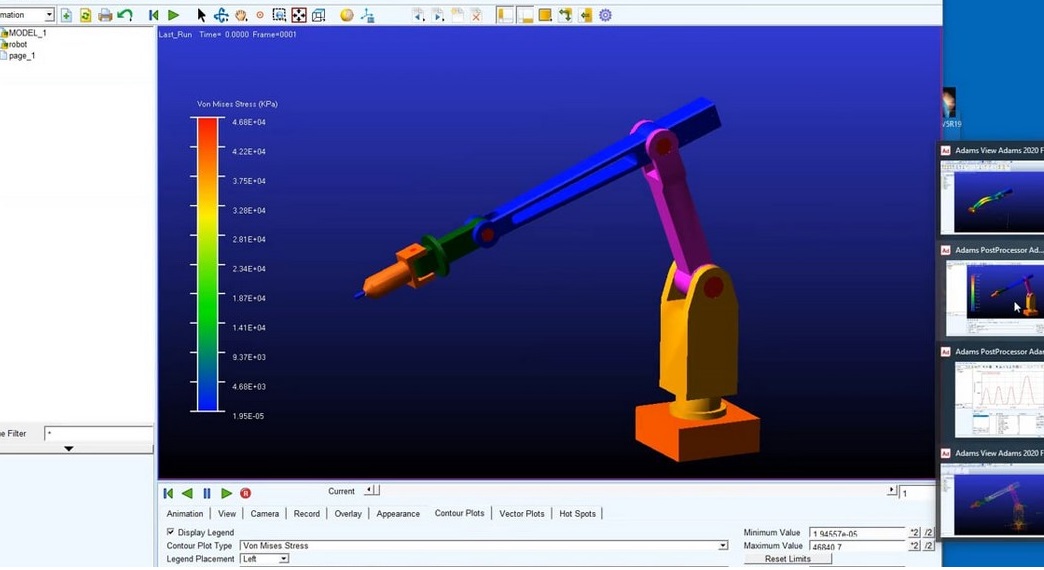
How & Why with Adams Flex

How To and Why To use Flexible Members in Mechanical System Design

System dynamics is very important in the design of mechanisms – ignoring dynamic effects and flexibility in your system by simulating mechanisms using simple kinematics such as the tools in your CAD system, can lead to problems in behaviour downstream - as this short video illustrates.  

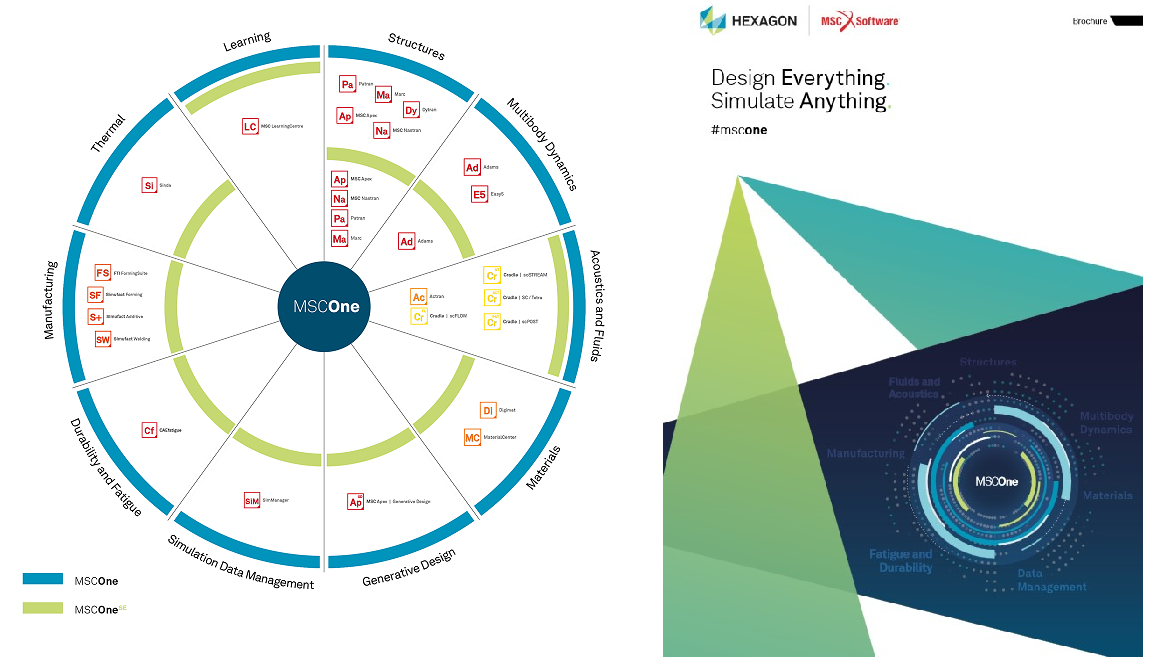
Unboxing MSC One

The MSC One Method

With MSC Software's subscription based token system, you receive a pool of tokens. Your tokens are checked out from the pool and are used to access and run a full range of CAE solutions available under the MSC One licensing system from MSC Software. Each individual software item requires a certain number of tokens to run. After each use, your tokens are returned to the pool for other use. There are dozens of software items available under MSC One.

Predicting Flowrate with scFLOW

CFD demonstration

A common use of Computational Fluid Dynamic (CFD) is in the design of fans and pumps.  This short video demonstration shows how simple it is to set up a centrifugal fan model in scFLOW. 

In this example we are looking to predict the flowrate throughput for a given fan speed, which is easily done by following steps in the wizard driven interface.